VGG
ResNet 原论文链接,为了解决在传统网络的层数太深的时候,就会发生梯度爆炸、梯度消失以及退化情况,然后下面是原论文中给出的ResNet的两个主要内容:
- 残差结构使得搭建超深层网络结构成为可能,能够解决退化问题;
- 使用Batch Norm来加速训练,可以解决梯度消失和梯度爆炸的问题。
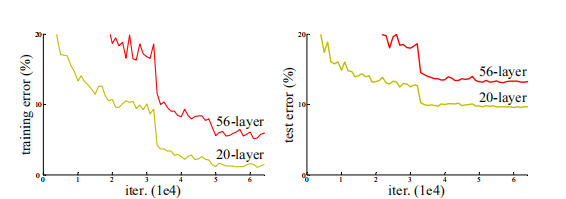
其中退化问题,可以简单理解成当网络越深时,准确度出现饱和,甚至出现下降,如下图所示,接下来,我将详细介绍一下残差结构和Batch Norm。
1. 残差结构:
1.1 残差块:
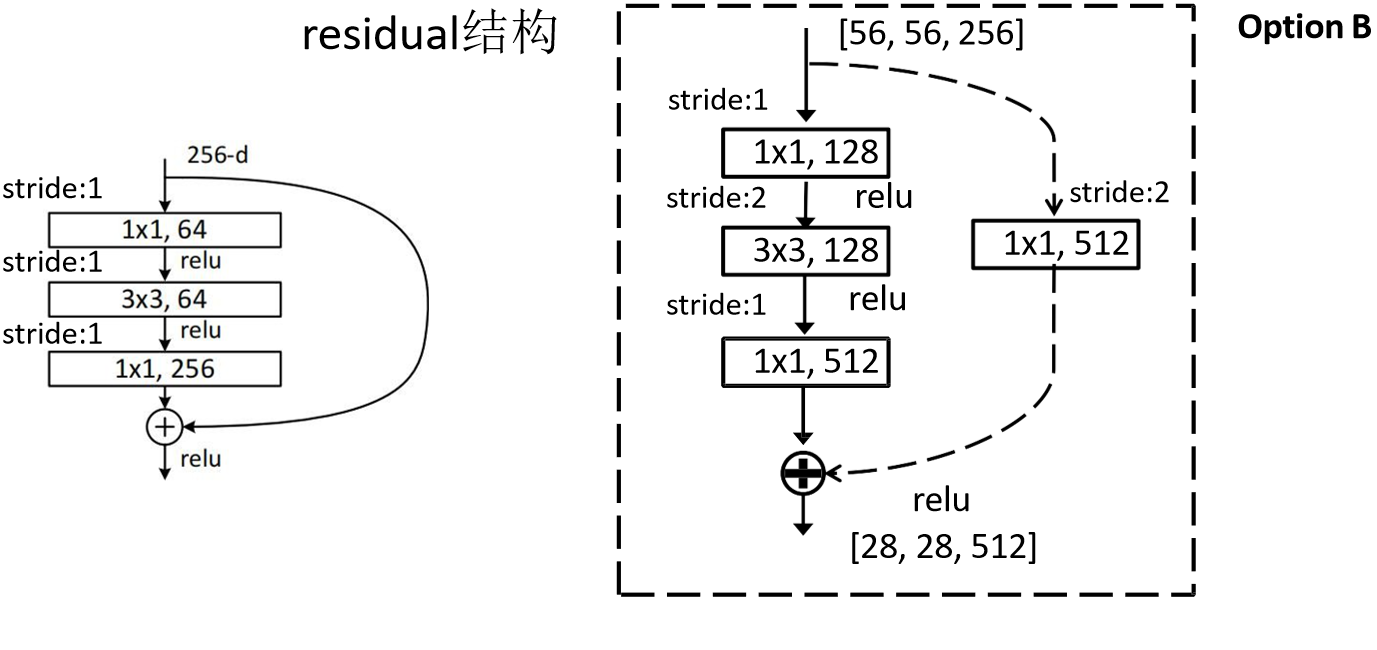
下图中的两个残差块结构,左边结构主要是使用在ResNet-18 和 ResNet-34,右边的结构主要是使用在更深层的ResNet-101和ResNet-152。
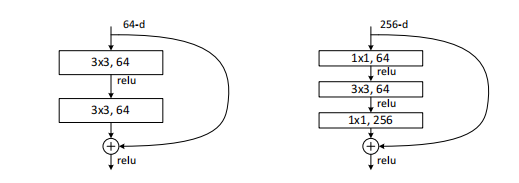
简单来看一下,这个模块的结构,就是分为直线(卷积+relu)和曲线,曲线这里就可以理解成对块输入啥都不操作,直接拿过来和块最后卷积的输出进行相加/concat,所以这里就要注意要保证concat的两个输入尺寸相同,也就是块中最后一层卷积的输出要和块的输入尺寸相同。
至于为啥深层的ResNet使用右边的这个残差块,我觉得是参数计算量要小很多,可以通过输入尺寸为(3,256,256)来计算一下,这里注意要保证上述提到过的条件外,同时还得保证最终两块feature map尺寸相同,所以就得把左侧层数调整为256,计算结果为:
左:3×3×256×256+3×3×256×256=1,179,648
右:1×1×256×64+3×3×64×64+1×1×64×256=69,632
很明显,右侧运算次数要远少于左侧的。下图是ResNet-34的整体结构,但是可以发现,里面怎么还有曲线部分还有虚线的,下部分就来说一下,虚线和实线的区别:

1.2 Residual Block:
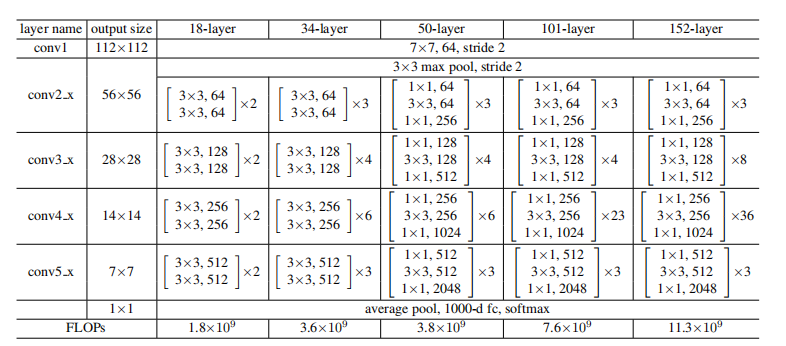
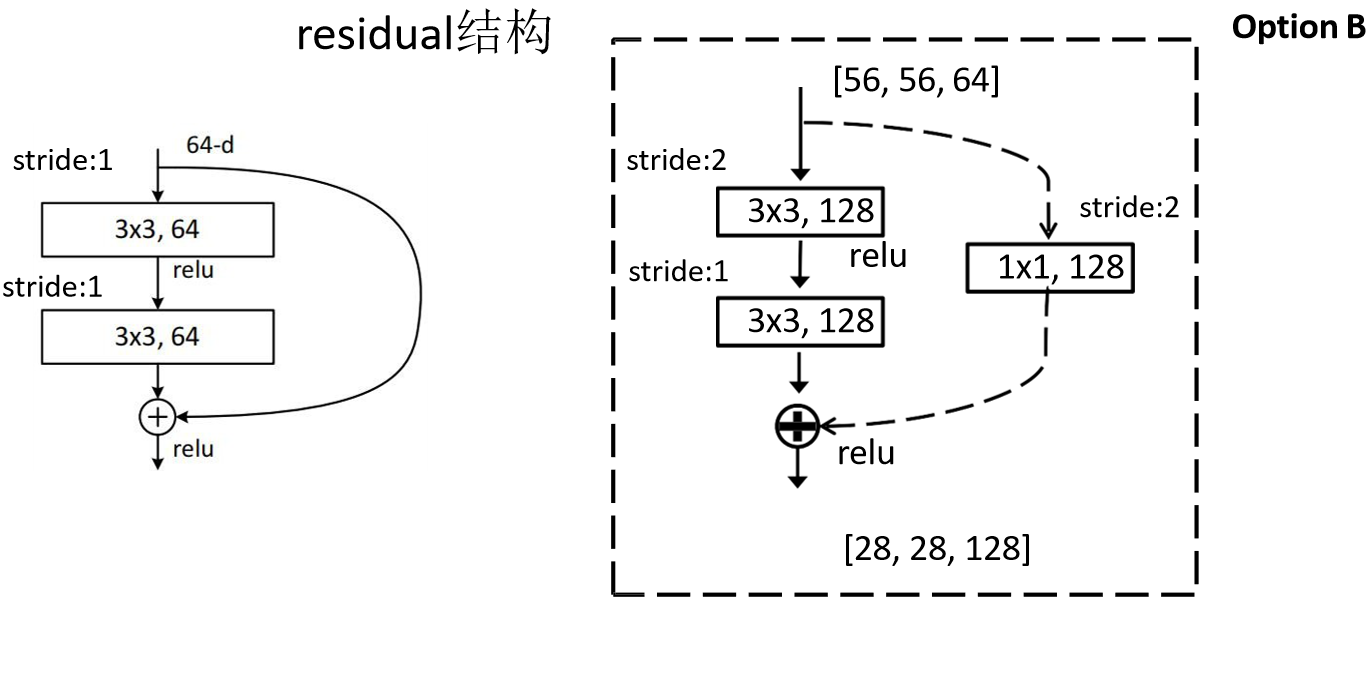
首先来看下,原论文中给出常用ResNet网络结构参数,可以看到output size那里,每一层feature map的size都缩小为之前的1/2,而我们通过计算可以知道,conv2_x那里的缩小是因为max pooling操作导致的,而下面的conv3_x、conv4_x、conv5_x,则是通过blocks中的第一个block来减小了feature map的size,同时扩大的channel数。也就是说,conv3_x、conv4_x、conv5_x中的blocks的第一层都是下两图中右半部分的结构。至于为啥stride=2,就缩小为1/2,根据out = ( in+2*padding-kernel_size )/stride+1计算,就可以得到。当然了这里仍然要保证输入输出的尺寸相同,因此虚线部分也要扩大channel。
2.批量归一化:
2.1 BN:
Batch Norm的主要目的是让feature map满足方差为1、均值为0的分布,下图的蓝框是原论文中的描述。

首先给一个使用顺序:conv=>bn=>acn,假如输入$X$(维度为$[C,H,W]$),在经过卷积操作后得到的输出$Y=w·X+b$,会随着网络层数的加深or在训练过程中,其分布发生偏移,向着即将要进入的非线性激活函数作用域的上下限靠近,例如sigmoid函数就是在x的很大正值or负值位置,这些位置导数接近于0,因此就会发生梯度消失的情况,从而导致神经网络的训练收敛变慢。而BN就是通过将跑偏的分布拉回到方差为1、均值为0的正态分布,也就是说使得非线性激活函数的输入值位于其有效作用域之间,因此在输入发生一个小一点的变化时,也可以使得损失函数有较大的变化,从而增大梯度,避免梯度消失的问题,并且加快网络模型学习收敛速度,从而加快训练。

下面,根据上图给出BN的计算公式接着说,首先前三个公式,计算一个batch中所有样本的方差$\sigma_B^2$和均值$\mu_B $,然后用每一个样本减去其均值$\mu_B $,最终除以平方差$\sqrt{\sigma_B^2+\epsilon}$,($\epsilon$是一个非常小的值,主要就是为了防止出现方差$\sigma_B^2$为0的情况),然后就得到了符合方差为1、均值为0的分布。
这里借用一下,一位大佬博客里的图(之后补上引用链接),这个例子计算的很清晰。
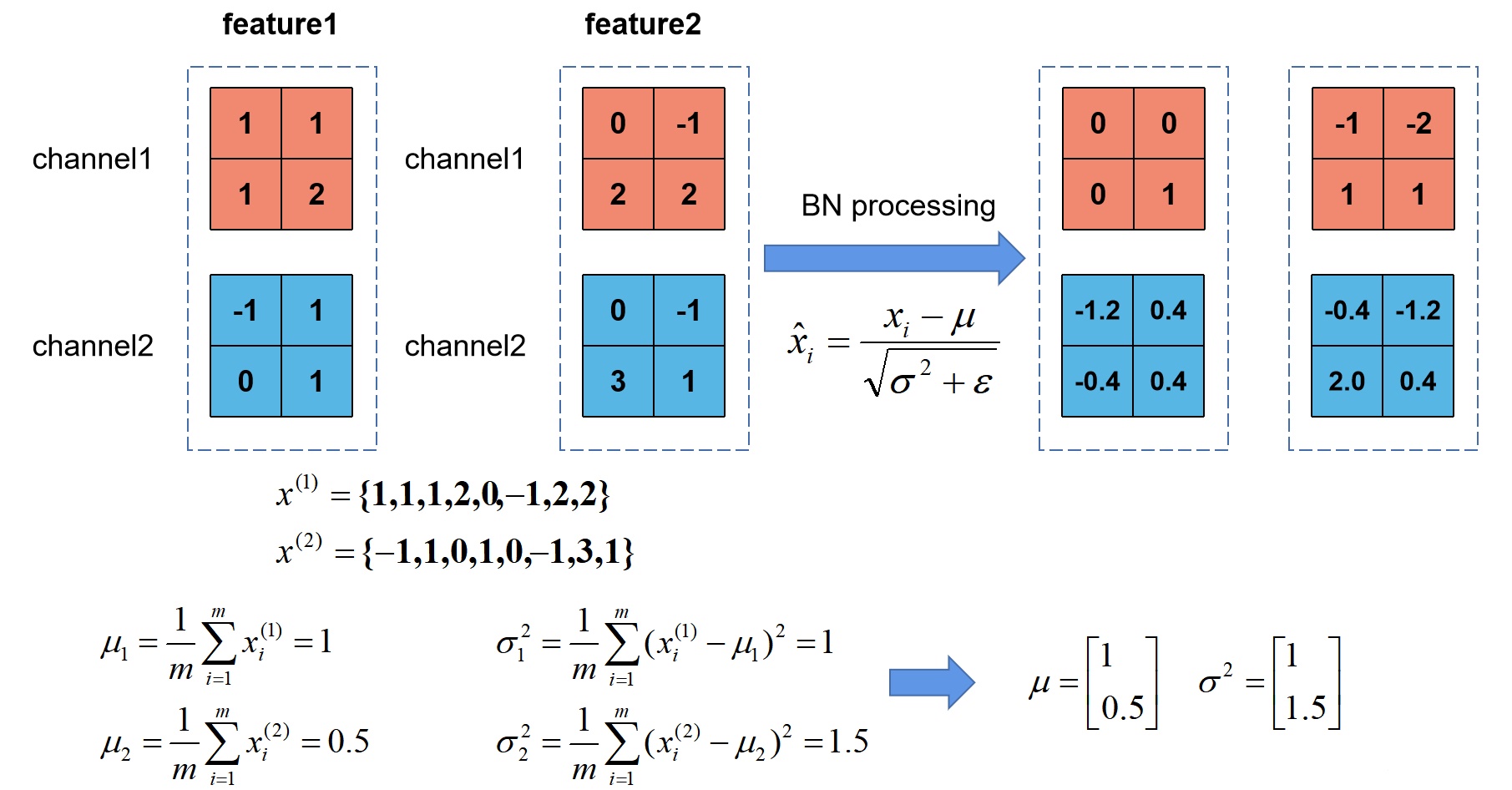
但是通过上面的描述,会发现这样都通过BN之后,那非线性激活函数不就几乎等同于线性函数了么,网络的深度也就失去了意义,因此BN为了保证非线性的效果,就对变换后的x,进行了scale and shift操作,通过$\gamma$和$\beta$来调整,它俩的初始化可以分别是1和0,然后再通过反向传播进行调整,也就是等价于非线性函数的值,从中心往周围挪了一下。因此BN最终可以享受到非线性的好处,又可以避免因太跑偏而导致的收敛速度慢。
训练过程中一个batch的$X$(维度为$[B,C,H,W]$),BN作用的范围就是$[B,H,W]$,而在测试的时候方差$\sigma^2$和均值$\mu $则是将训练过程中的所有batch的均值和方差保存起来,求均值的期望和方差的无偏估计(公式表达如下),也就是说test时,BN参数要固定,并且eval模式要打开。
\[E[x]=E_B[\mu_B]\] \[Var[x]=\frac{m}{m-1}E_B[\sigma^2_B]\]最后说下,为啥现在的卷积网络dropout的使用逐渐在变少,首先BN和t一样拥有正则化功能,而dropout在卷积上的正则效果是有限的,此外卷积相对全连接层而言参数量更少,而且激活函数也可以完成特征的空间变换,而dropout表现很好的全连接层,它的作用正在被全局平均池化代替,因为后者不但可以减少模型大小还可以提高模型的表现。
上面说了BN测试和训练时候的区别,这里也简单补充下Dropout的吧,Dropout在训练时就是按照失活概率p(0-1),对这一层的神经元按照p的概率进行失活,也就是失活神经元的输出为0,恢复失活神经元(失活神经元保持原状,未失活神经元更新),然后对第二层输出数据除以1-p之后再传给下一层,作为神经元失活的补偿,因为在测试的时候是不会有dropout的,因此如果不除的话,就会导致下一层的输入和期望会有差异。
2.2 对比:
下图为常见Norm操作的作用情况,这里就简单做个比较,之后用空再详细展开。
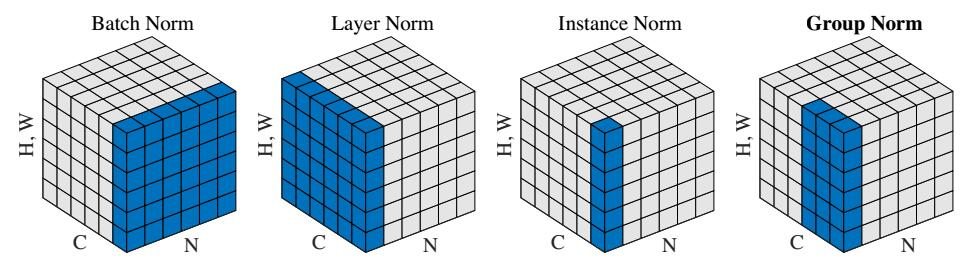
| 名字 | 作用位置 | 作用维度表示 |
|---|---|---|
| BN | batch | B,H,W |
| LN | channel | C,H,W |
| IN | channel内 | H,W |
| GN | channel分为group,group | C//G,H,W |
这里就简单插一句,LN在之后所写的Transformer中有所提到,BN在batch size较小的时候,这个batch的数据的方差和均值代表性就比较差,而在目标检测、分割等输入图像较大、维度较多,batch size一般都比较小,因此GN的效果会更好一些。
文档信息
- 本文作者:Guoziyu
- 本文链接:https://mateguo1.github.io/2020/08/15/VGG/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)