Loss function for semantic detection
[TOC]
整理一下语义分割中常用的loss function的公式和相关知识。
1. cross entropy loss:
交叉熵损失函数,先来看下二分类的binary cross entropy loss的公式表达:
\[loss = -\frac{1}{N}\sum{_{i=1}^{N}}(y_ilog(\hat{y_i})+(1-y_i)log(1-\hat{y_i}))\]其中N为像素点个数,$y_i$是输入$x_i$的真实类别,而$\hat{y_i}$是输入$x_i$的预测结果属于类别i的概率,下面就扩展到多分类的交叉熵函数公式表达,其中新增的m为类别数。
\[loss=-\frac{1}{N}\sum{^N_{i=1}}\sum{_{j=1}^m(y_{ij}log(\hat{y_{ij})})}\]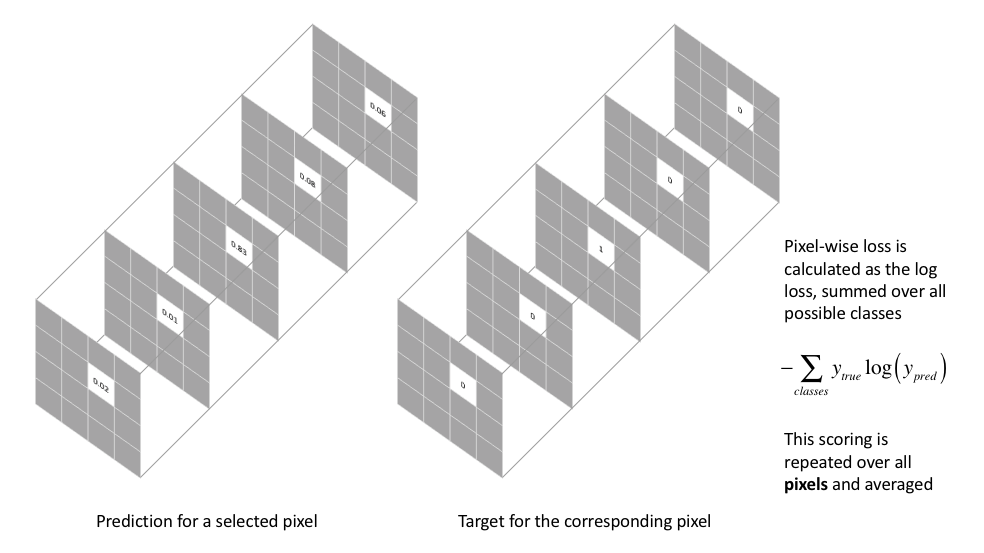
2. weighted loss:
因为交叉熵损失函数会评估每个像素点的类别预测,然后做总和的平均,因此这实质上是对图像中的每个像素进行平等的学习,但是如果不同的类在图像中的分布不均衡,这就有可能导致训练的时候由所占像素点比较多的那一类来主导,因此最终学习出来的特征就更偏向于这些类。
FCN和U-Net对上述问题,提出对于输出概率分布向量中的每个值进行加权,也就是希望模型能够通过关注数量更少的样本,从而缓解类别不均衡的问题,公式表达为:
\[loss = -\frac{1}{N}\sum{^N_{i=1}\sum{^m_{j=1}}(\omega_jy_{ij}log(\hat{y_{ij}}))}\]其中的$\omega = [\omega_1,…,\omega_m]$为对预测概率图中每个类别的权重,用在加权在预测图上占比较小的类别对loss的贡献程度,其公式表达为:
\[\omega_j = \frac{N-\sum{_i^N\hat{y_{ij}}}}{\sum_i^N\hat{y_{ij}}}\]3. focal loss:
直接上公式:
\[loss = -\frac{1}{N}\sum_{i=1}^{N} ( \alpha(1-\hat{y_i})^{\gamma}log(\hat{y}_i)y_i+(1-\alpha)\hat{y}^{\gamma}_{i} log(1-\hat{y_i})(1-y_i))\]$\hat{y_i}$是类别的预测概率,$\gamma$是大于0的值,$\alpha$是个0-1之间的小数,二者都是固定值,不参与训练。
这里主要涉及到背景和前景两者之间的区别, 说白了就是前景类使用$\alpha$,背景类使用$1-\alpha$,目前在图像分割上只适用于二分类。
4. soft dice loss:
基于Dice系数的损失函数,其本质是两个样本之间重叠的度量,范围为0-1,1表示为完全重叠。Dice系数可以表示为:
\[Dice = \frac{2|A\cap B|}{|A|+|B|}\]A、B分别表示两个集合,然后soft dice loss表示为:$1-Dice$,最终的loss表示为:
\[loss = 1-\frac{1}{m} \sum{_{j=1}^m} \frac{2\sum_{i=1}^Ny_{ij}\hat{y_{ij}}}{\sum{_{i=1}^Ny_{ij}}+\sum{_{i=1}^N\hat{y_{ij}}}}\]这种方法比较适用于样本极度不均的情况,而一般情况下,使用它会对反向传播造成不利影响,而且该方法好的模型并不一定在其它的评价标准上效果更好,使用它有时会使得训练曲线不可信,主要原因是对比softmax和log loss的梯度简化来讲是p-t,t为目标值,p为预测值,而该方法为$\frac{2t^2}{(p+t)^2}$,如果p、t过小会导致梯度变化剧烈,从而使得训练困难。
文档信息
- 本文作者:Guoziyu
- 本文链接:https://mateguo1.github.io/2021/03/15/loss-function/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)