UNet

U-Net作为一个强大的语义分割模型，论文链接，可以通过使用较少数据进行训练即可得到不错的效果，下图是原论文中给出的U-Net的网络结构，概括为encode+decode，下图中主要把它从左到右分为三个部分：encode、decode、output，其中encode与decode之间的连接关系包括直接concat和bottleneck。

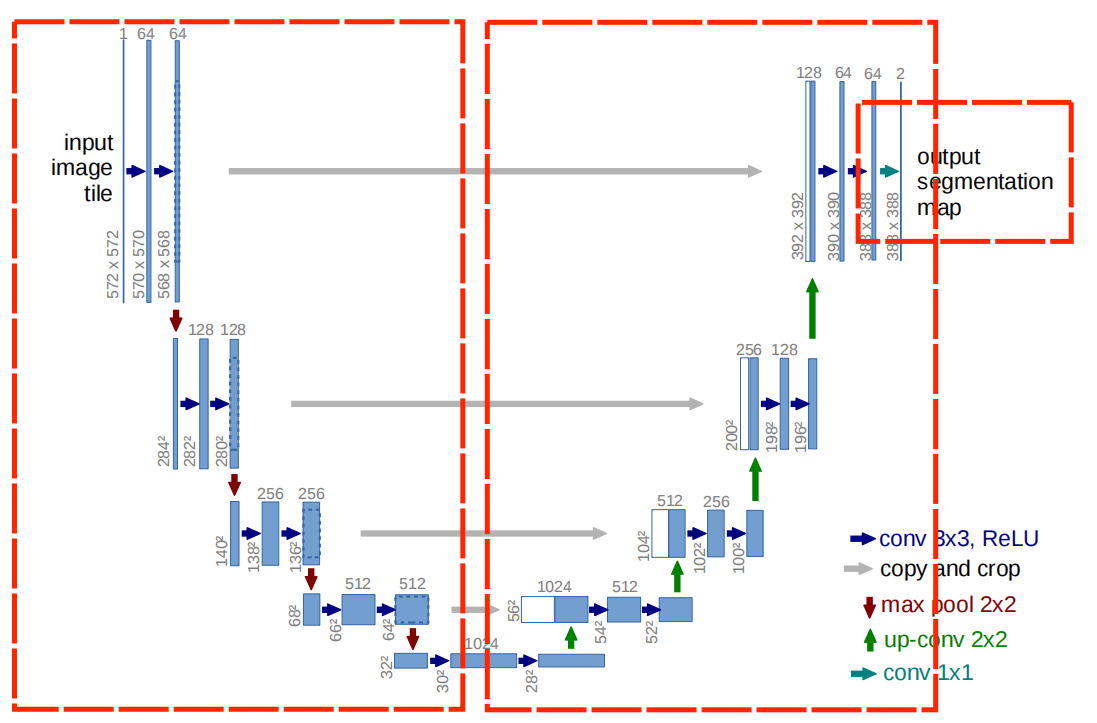
1. U-Net：

1.1 Encoder和Decoder：

上图中的最左边的框框里，按照图里的顺序命名为encoder1-4、decoder4-1和encoder5吧，其实这个结构可以概括为卷积与最大池化的堆叠，当然了encoder的结构也可以换成VGG、ResNet等网络。

encoder1-4输出的feature map，都会被当作下一层的输入，并且和对应decoder里面的部分进行特征融合（上采样+堆叠），decoder5-2输出的feature map，也都会当作下一层的输入，并于encoder对应的部分进行特征融合，至于卷积核尺寸和特征图的层数图上都表明的很清楚了，这里就不在赘述了，哈哈哈哈。

1.2 转置卷积：

这里使用了逆卷积来进行上采样，除逆卷积之外，我还看到好多人用了双线性插值（这个貌似是得改通道数），之后再把双线性插值补上，这里贴上两个官网给出的链接：逆卷积动图，逆卷积论文，非常值得参考，下面我简单的概述一下。

# pytorch官网源码
#https://pytorch.org/docs/stable/generated/torch.nn.ConvTranspose2d.html#torch.nn.ConvTranspose2d 

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)
# 这里是pytorch官方给出的代码
torch.nn.ConvTranspose3d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)

# 具体参数解释
#in_channels (int) – 输入图像中的通道数
#out_channels (int) – 卷积产生的通道数
#kernel_size (int or tuple) – 卷积核的大小
#stride (int or tuple, optional) – 卷积的步幅。默认值：1
#padding (int or tuple, optional) – dilation * (kernel_size - 1) - 零填充将添加到输入中每个维度的两侧。默认值：0
#output_padding (int or tuple, optional) – 添加到输出形状中每个维度一侧的额外尺寸。默认值：0
#groups (int, optional) – 从输入通道到输出通道的阻塞连接数。默认值：1
#bias (bool, optional) – 如果True，则向输出添加可学习的偏差。默认：True
#dilation (int or tuple, optional) – 内核元素之间的间距。默认值：1

先简单地总结一个泛化的实现思路：（建议对比着动图看，蓝色是输入，绿色是输出。）
（1）对于输入的特征图A进行一些变换，得到新的特征图A‘；
（2）对新的卷积核进行设置，得到新的卷积核设置；
（3）用新的卷积核在新的特征图上做正常的卷积操作（stride为1），即可得到最终的结果。

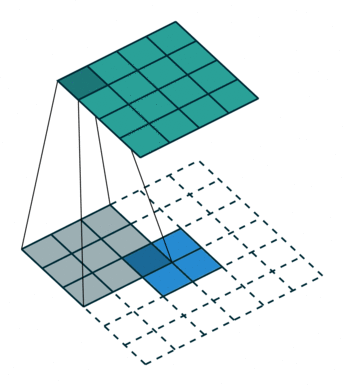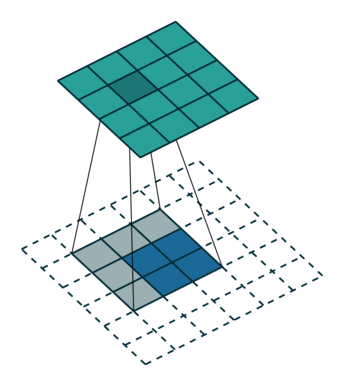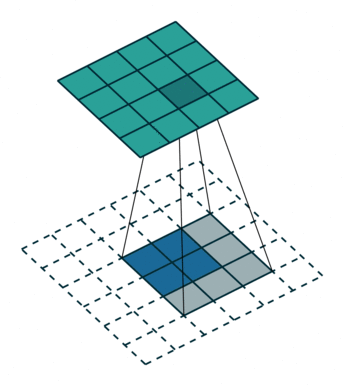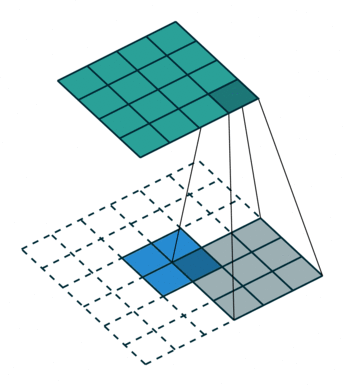
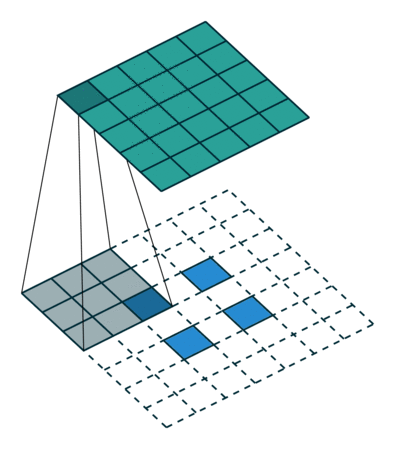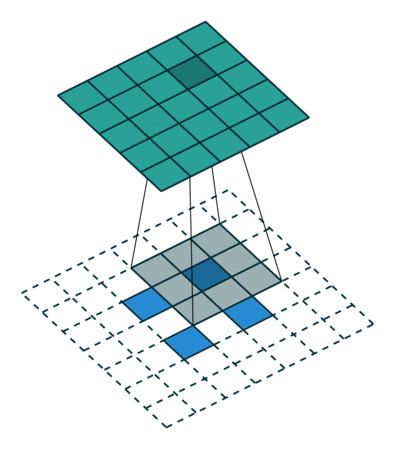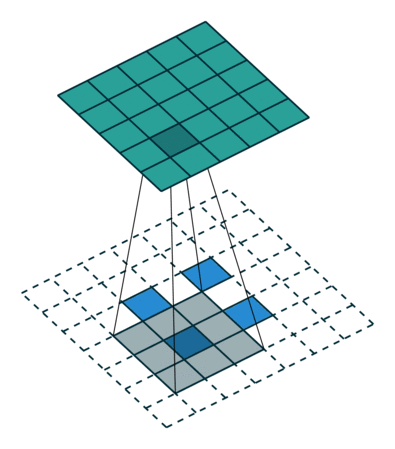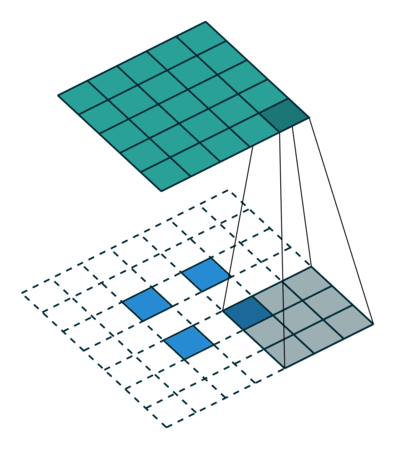
假设输入为特征图A（H，W），下面用H的处理过程进行举例，W同理。 首先，只考虑stride，对A进行插值（interpolation），在A的高度方向每行都插入一行0，共插入$stride-1$行0，上图左侧stride为1（这是最基础的转置卷积，可以先无视外面的虚线框，下面就会讲明），右侧stride为2。

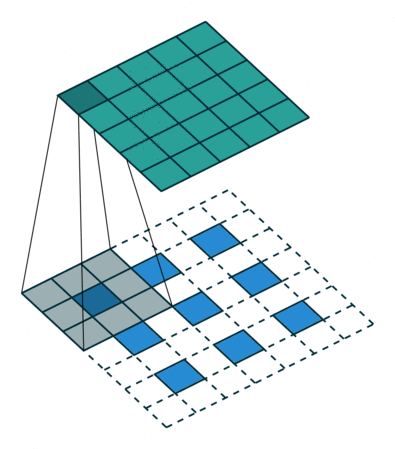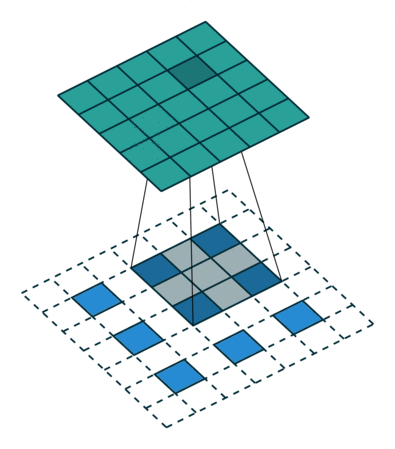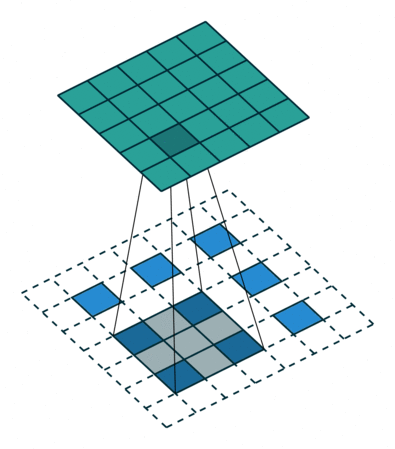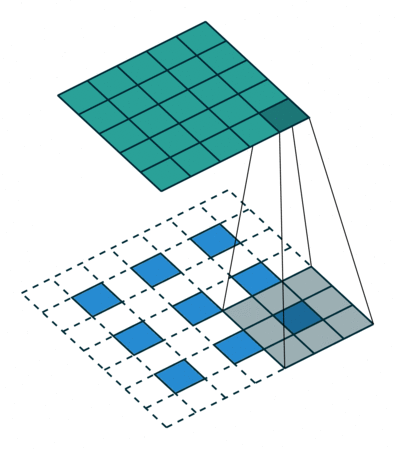
然后，再来考虑padding，对A进行填充，在其外侧，填入$kernel_size-padding-1$圈0，这也就解释清楚了，最基础的转置卷积那张图的虚线框了，上图左侧的padding为2、stride为1，右侧则是再加上了stride的形式。

那么即可得出结论最终输出的高度计算公式为：$H_{out} = \frac{[H_{in}+(stride-1)+2\times(kernel_size-padding-1]}{stride’}+1$，当然了这里的$stride’=1$，所以增大padding会让最终输出的图像大小减小，下面是官网给出的关于ConvTranspose3d的公式：

可以运行下面的代码，来理解

import torch
from torch import nn
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[1.0, 1.0, 1.0], [1.0, 1.0, 1.0], [1.0, 1.0, 1.0]])
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 3, 3)
# 注意kernel_size-padding-1不能小于0
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, padding=0, bias=False)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=1, padding=0, bias=False)
# tconv = nn.ConvTranspose2d(1, 1, kernel_size=1, padding=1, bias=False) 
tconv.weight.data = K
y = tconv(X)
print(y)

1.3 参考代码：

U-Net_Colab

2. mIOU：

2.1 简述：

均交并比：Mean Intersection over Union

首先来看下IOU，下图黄色部分代表label，蓝色代表prediction，其中相交部分即为TP，有颜色的区域为二者相并，而mIOU就是该数据集中的每一类的交并比的平均。

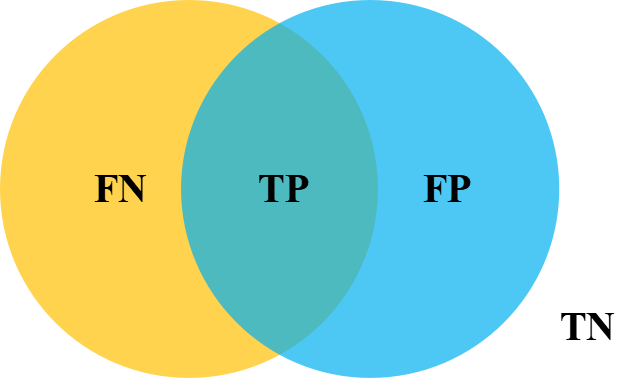
2.2 计算

（1）混淆矩阵：

行之和为该类的真实样本数量，列之和是预测为该类的样本数量（随便编的一个矩阵）

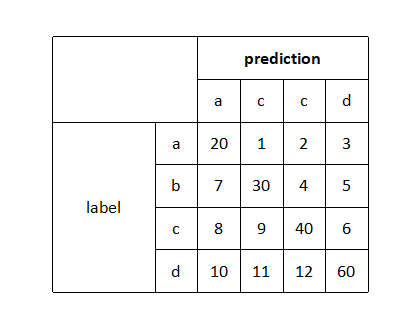
（2）计算mIOU：

针对于每一类IOU：
交：对角线的值
并：行+列-对角线值 IOU=交/并 mIOU=mean(sum(IOU))

3. ResNet+U-Net

用pytorch中的ResNet作为encoder替换U-Net原始结构，可以用ImageNet的预训练权重来fine-tuning，下图是ResNet原论文中的结构。

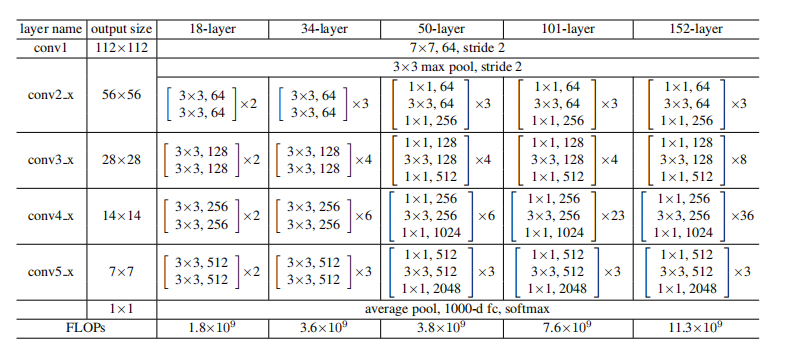
下图是pytorch官方的ResNet34的源码，然后colab的代码，如下。

ResNet_UNet_Colab