Graph Convolutional Networks

1. 简单粗暴的理解一下原理：

本段内容，整理自B站up主小淡鸡的视频，链接如下：

GNN：https://www.bilibili.com/video/BV1Xy4y1i7sq?share_source=copy_web GCN：https://www.bilibili.com/video/BV1Xy4y1i7sq?share_source=copy_web

1.1 Graph Neural Networks, GNN:

先来简单解释一下图神经网络，主要流程就是：聚合、更新、循环。

首先讲解下聚合，可以看到下图的图结构中一共包含A、B、C、D、E、F六个点，而点与点之间的连线就代表着这两点之间有某种联系，而每个点右下角的(X,X,X,X)用于表示该点的特征，这个特征可以是提取到的或者是标签，也可以是初始化的，这里其实把现在图上的特征说成初始特征，更利于后面内容的区分和理解。

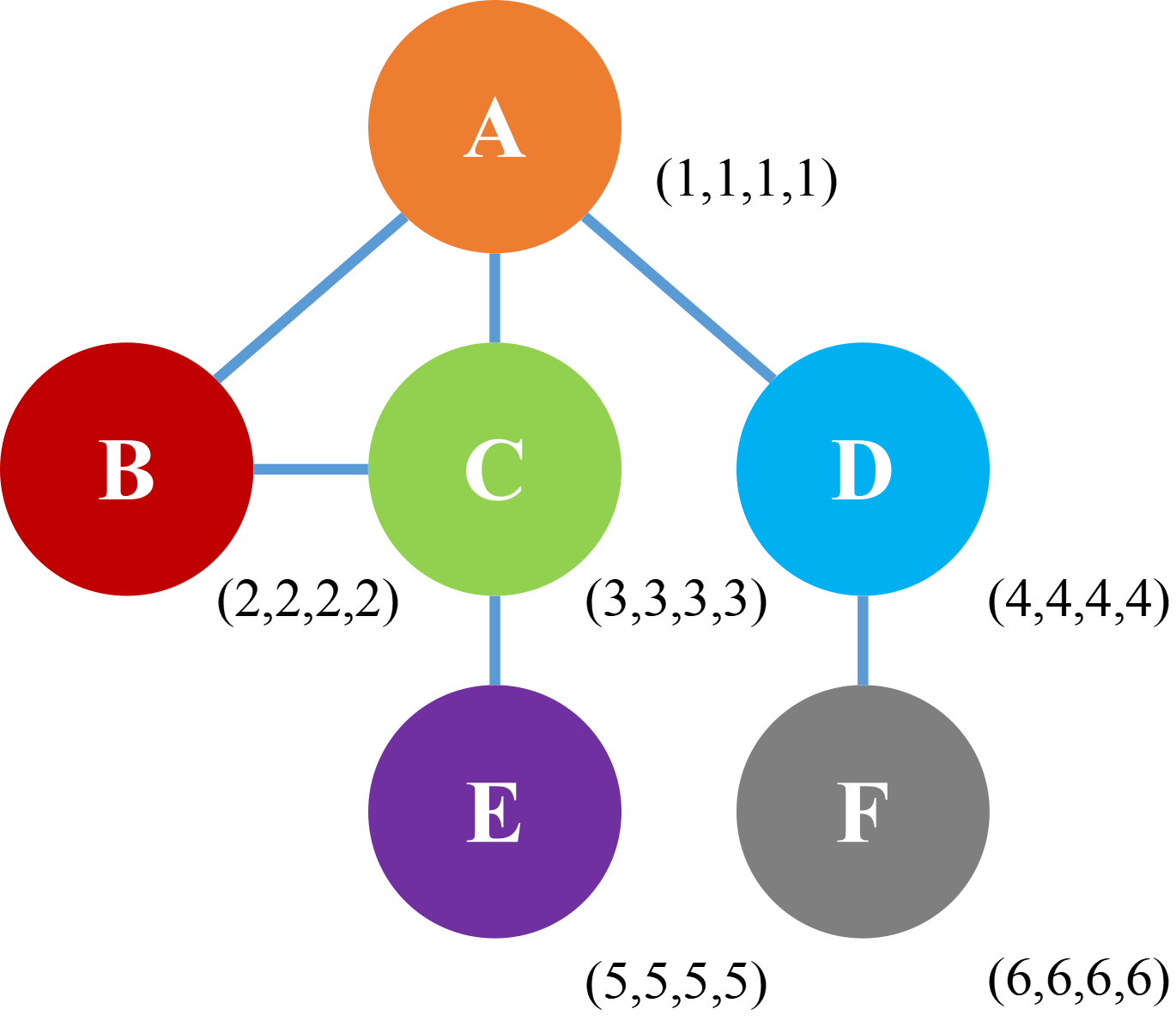
接下来，假设我们要对A进行分类，这就需要得到它的特征，而A的特征由两部分组成：自身+邻居信息。这里简单解释下为什么邻居信息会组成A的特征，介于上面提到的点与点之间有连线，说明这俩点之间有某种关系，所以说如果对A进行分类/定义，某种程度上而言，它的邻居B、C、D的特征也具有一定的参考价值，然后再用一句话来解释一下，就可以很明白的理解了，“近朱者赤，近墨者黑”。

最后可以把邻居信息N，用公式表示为，N = a*(2,2,2,2) + b*(3,3,3,3) + c*(3,3,3,3)，其中的a、b、c大概就是超参数，可以进行优化、改进。

然后就到了更新的阶段，将更新后A的信息用公式表示为 A_new = σ(W((1,1,1,1))+σ*N)，其中的σ表示激活函数，W( )为模型训练的参数。

然后再来说下GNN层数的一个点，让我们把目光重新放回到上面的那张图中和点A相连的点有B、C、D，也就是说A包含B、C、D的信息，所以我们就可以知道，而B包含A、C的信息，C包含A、B、E的信息，D包含A、F的信息。那么在第二层，也就是第二次聚合时，聚合A的信息，现在A已经包含了C的信息，而C中又包含了E的信息，所以A也就会获得E的特征，然后就可以得到每一个结点的最终特征，然后就可以进行结点分类或者关联预测了。

1.2 Graph Convolutional Networks, GCN:

图卷积神经网络，主要流程还是：聚合、更新、循环，而它与GNN之间的主要区别就在于聚合过程。首先，GCN就是为了解决GNN中邻居信息的公式里a、b、c值的设定，然后我们根据上面GNN的讲解来看，首先提出一个平均法，举个栗子就是：你认识的人工资的平均值=你的工资，然后可以你的工资用公式表示为：

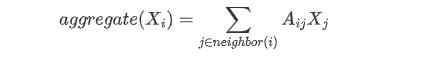
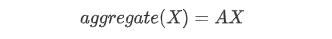
但是上述公式忽略了自身的特征，针对于工资我们可以举例：学历、工作等，然后我们需要添加一个自环把自身特征加回来（单位矩阵），变成如下的公式：

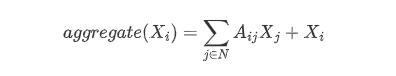
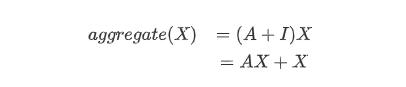
然后再求一个平均，引入度矩阵D，得到公式如下：

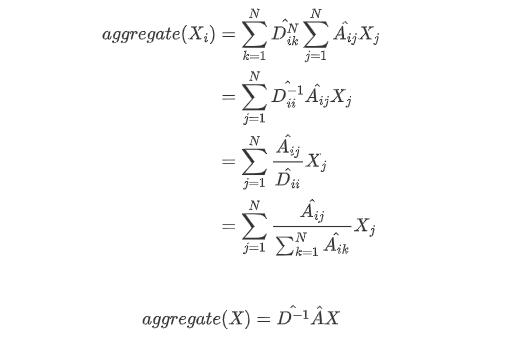
但是平均法有一个问题，我们来看下图，图中点A只与点B相连，而B与C、D、E等等相连，那么A的度就是1，带入到上述公式就是1/1的B的特征，所以说直接聚合B的特征来参考A，就有失偏颇了。

GCN为了解决上述这个问题，提出了如下的公式：

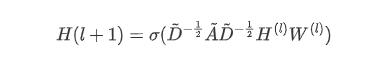
该公式中 H(l) 代表当前层的特征， W(l) 就是要求的参数，而A为邻接矩阵（n×n）、D为度矩阵（n×1，也就是把邻接矩阵进行行求和），借用GNN中所用的图，表示如下图所示：

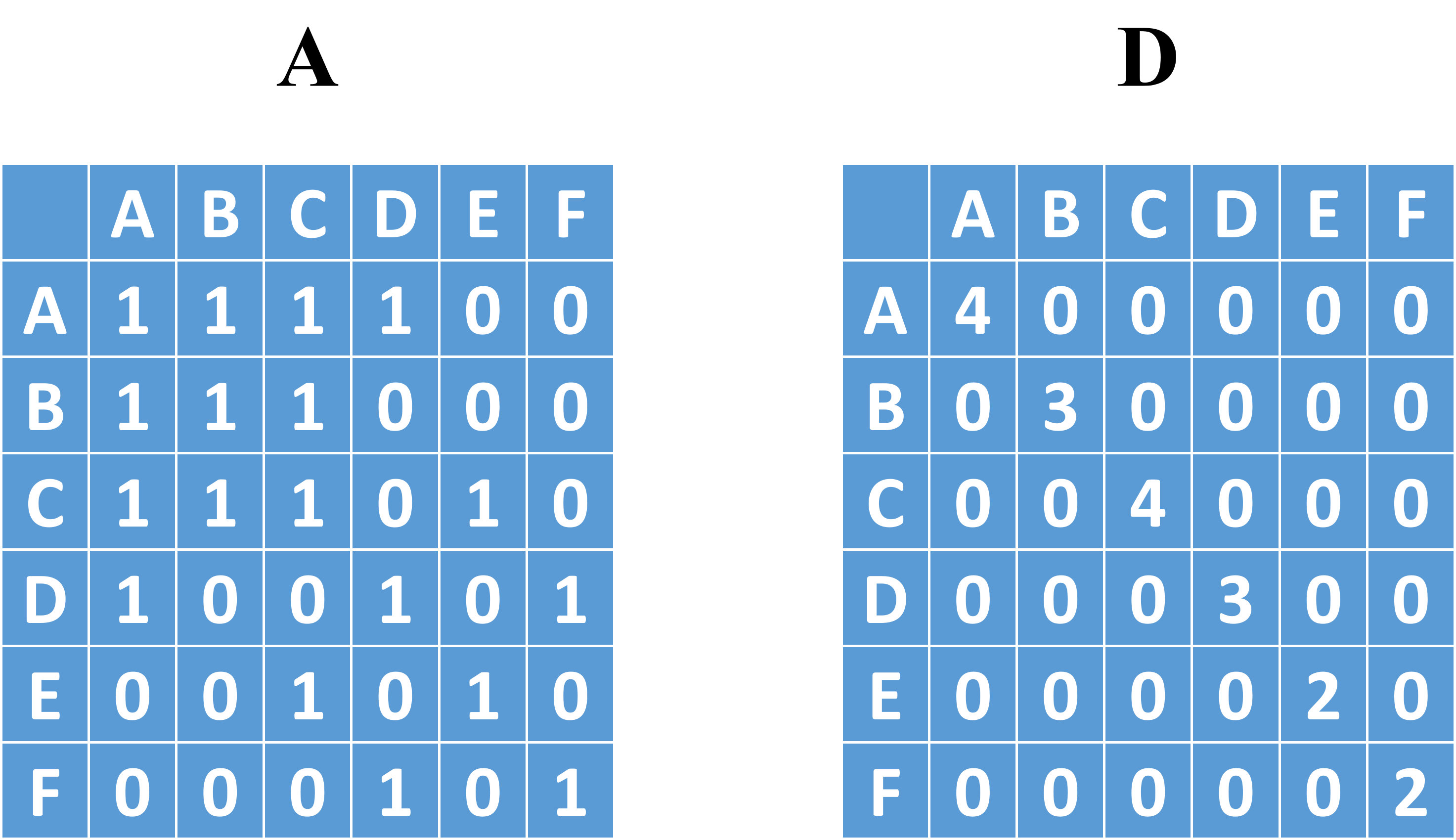
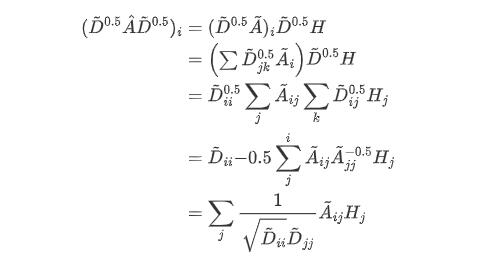
我们把上面的图-1，i当作点A，j当作点B，然后对应的D值分别为1和9，所以B在发散时，就不会完全把B的信息加载到A上，对称归一化拉普拉斯矩阵，解决了差距大的问题。度矩阵其实是一个归一化的操作，如果A矩阵相乘与H、W相乘就是得到了A邻居的特征，而A+I（单位矩阵）再相乘就保证了聚合自身的信息了

邻接矩阵有一个问题是读入的时候是有向图，需要进行一步转置的操作变成无向图（也就是沿着对角线对称的那种），按行归一化，邻接矩阵归一化