Transformer:

今天新开一个坑（虽然之前好多坑都没填完，哈哈哈哈），论文链接Attention is All You Need。

接下来，先整理下李宏毅老师的ML课上讲的transformer，课件链接，然后这部分主要是课后的一些个人的思路总结，顺序上可能和课件不太一样，因此还是很建议大家直接去看课程视频，讲的太好了！（ps：由于是学习总结，所以会借用大量李老师课件里的图），下面整理的理论部分主要是参考李宏毅老师的，而代码部分主要用到了李沐老师的动手深度学习的内容，这是对应链接。

按惯例，直接来吧，先上网络结构，图0 是原论文中给出的模型结构，可以主要分为encoder和decoder，然后还有一个Input Embedding和Positional Encoding，下面就简单的梳理一下Transformer的整体思路和相关内容。

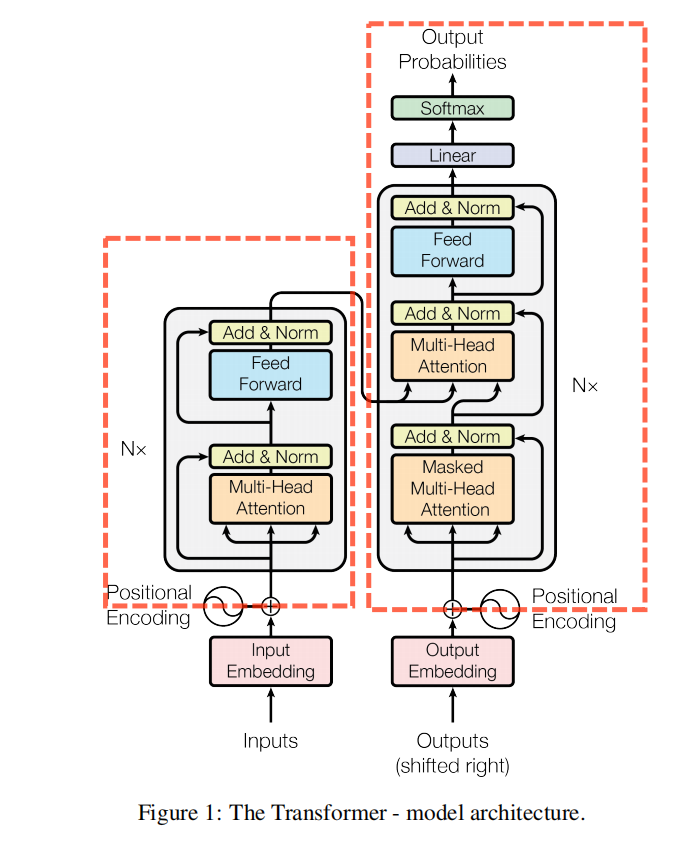
Transformer_0

图0.Transformer模型结构

1. Transformer：

代码部分：

import math
import torch
from torch import nn
from d2l import torch as d2l

1.1 Input Embedding：

将每一个词变成词向量。

1.2 Positional Encoding：

由于Transformer是为了处理机器翻译的，这个数据内部是包含时序关系的，而self-attention对比RNN（在模型内，考虑到前面输入部分的特征）而言是考虑不到数据的时序关系，因此Transformer使用了positional encoding，也就是在进入Encoder部分前，在输入中加入时序关系，说白了经过没有位置编码的SE而言，你好啊和啊好你，好得到的新向量是一样的。下面代码描述的是基于正弦函数、余弦函数的位置编码（vanilla）。

class PositionalEncoding(nn.Module):
    """位置编码"""
    def __init__(self, num_hiddens, dropout, max_len=1000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, num_hiddens))
        X = torch.arange(max_len, dtype=torch.float32).reshape(
            -1, 1) / torch.pow(10000, torch.arange(
            0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
        self.P[:, :, 0::2] = torch.sin(X)
        self.P[:, :, 1::2] = torch.cos(X)

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

输入为X，位置编码使用形状相同的位置嵌入矩阵P，输出X+P，而P矩阵上的第i行、第2j列和2j+1列上的元素公式表示为，其中行代表词元在序列中的位置，而列代表位置编码的不同维度：

\[p_{i,2j}=sin(\frac{i}{100000^{2j/d}}) \\ p_{i,2j+1}=cos(\frac{i}{100000^{2j/d}})\]

至于这里为什么加上PE而不是concat，我也不是非常清楚，现在大概理解了两个点（1）concat之后还是要进行线性变换的，所以最后作用还是变成了相加；（2）因为有残差链接，所以位置编码的信息不会消失。

1.3 Encoder：

图1.Encoder Block

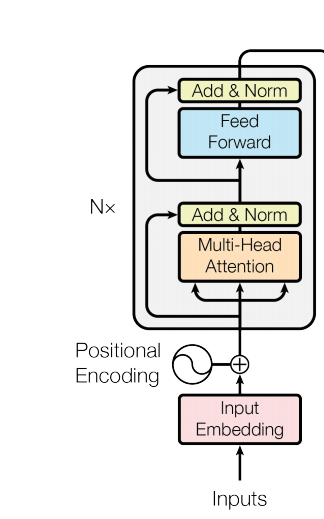
首先，从图1.的整体上来看Encoder结构，分为两部分MHA和FFN，它前面有一个N×（重复N次，论文里面是用的N=6），而这N个Encoder的结构是一样的，但其中的参数不同，从图2.中可以看到一个Encoder Block的结构分解为右半部分那样。MHA<=>Self-attention; FFN<=>FCs

图1-1

图2.Encoder Block

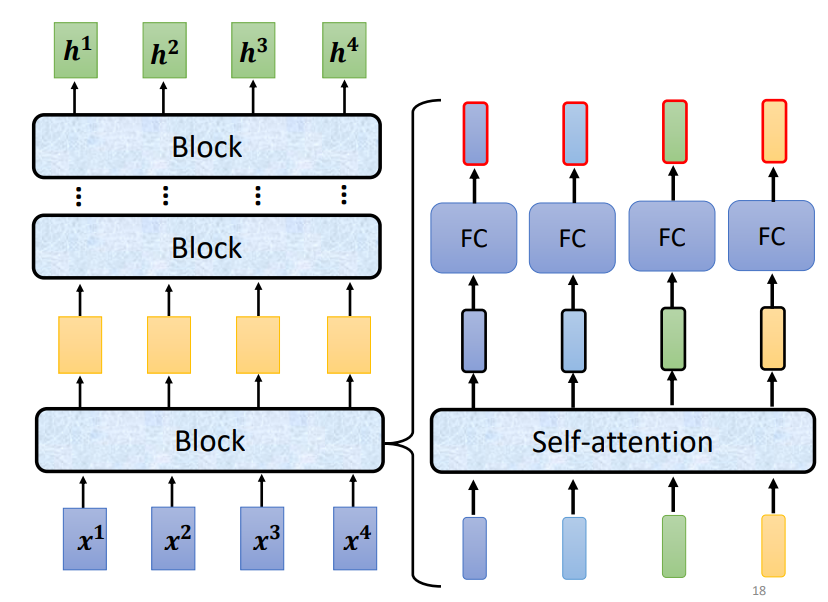
再来按顺序说明下Encoder Block的结构，首先是Multi-Head Self-attention，然后是Add+Norm，结构如图3.所示，分别为Residual和Layer Norm，最后还包括一个Feed Forward Network，下面首先将分开讲解这三个部分，然后最后再结合起来说明整个Block的结构。

图3. Add Norm

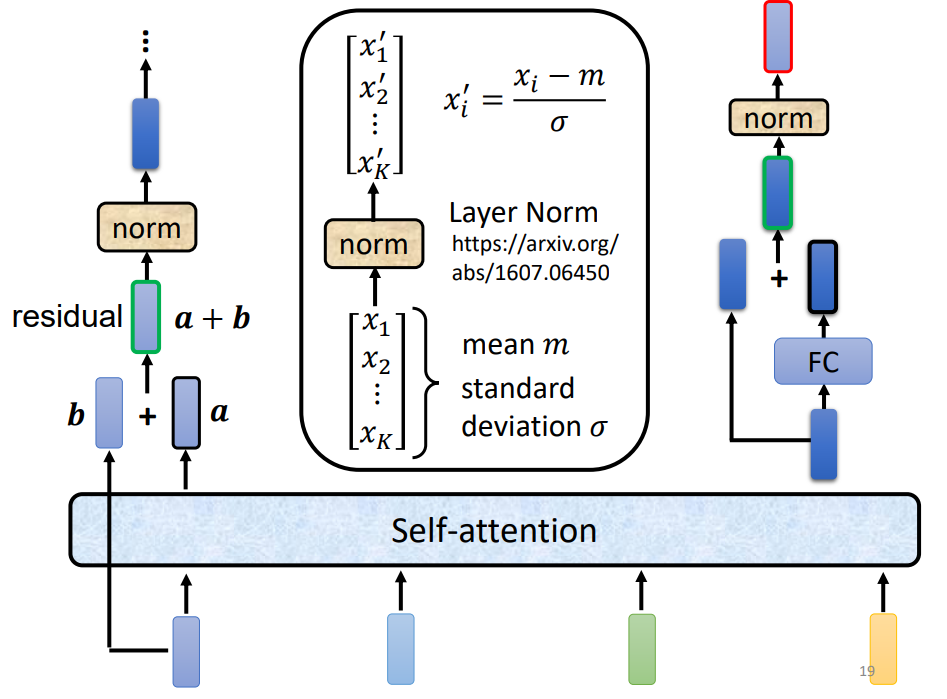
1.3.1 Add Norm：

1.3.1.1 Layer Norm:

对比一下batch norm（每一个特征进行规范化，减掉均值，除以方差，均值0，方差1），layer norm（每一个样本规范化），其在二维时，是将batch norm转置即可，而三维的话，切出来的是两个平面。

使用LN的原因主要为：时序数据的样本长度会变化，如果变化大，那么均值方差变化大，因此在遇到一个特殊的样本时，对它而言，BN就可能不那么好用，而LN是在样本里面算的，就没有这样的问题了。之后有论文对LN在梯度方面进行了分析，这里就不再深入讲解了（留个坑）。

ln = nn.LayerNorm(2)
bn = nn.BatchNorm1d(2)
X = torch.tensor([[1, 2], [2, 3]], dtype=torch.float32)
# 在训练模式下计算X的均值和方差
print('layer norm:', ln(X), '\nbatch norm:', bn(X))

'''
output:
layer norm: tensor(
		[[-1.0000,  1.0000],
        [-1.0000,  1.0000]], 
        grad_fn=<NativeLayerNormBackward>)
batch norm: tensor(
		[[-1.0000, -1.0000],
        [ 1.0000,  1.0000]], 
        grad_fn=<NativeBatchNormBackward>)
'''

1.3.1.2 Add Norm:

使用了残差连接（需要两个输入形状相同，就是相加）、LN来实现该类，代码如下：

class AddNorm(nn.Module):
    """残差连接后进行层规范化"""
    def __init__(self, normalized_shape, dropout, **kwargs):
        super(AddNorm, self).__init__(**kwargs)
        self.dropout = nn.Dropout(dropout)
        self.ln = nn.LayerNorm(normalized_shape)

    def forward(self, X, Y):
        return self.ln(self.dropout(Y) + X)

1.3.2 Multi-Head Attention：

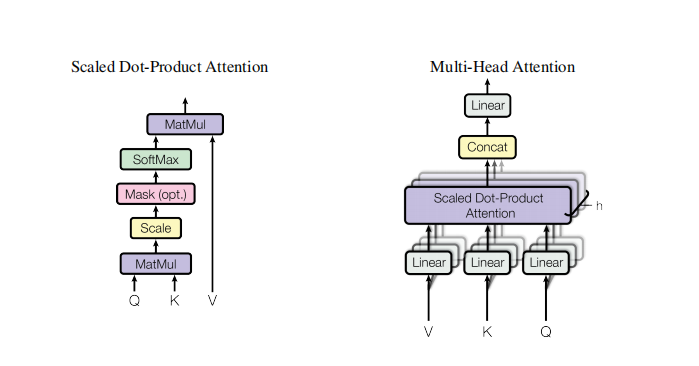
这部分涉及到了self-attention的部分，图4.是原论文中给出的Scaled Dot-Product Attention和Multi-Head Attention的结构，而接下来，我会先整理一下李宏毅老师的课里讲的self-attention（ppt：https://speech.ee.ntu.edu.tw/~hylee/ml/ml2021-course-data/self_v7.pdf），所以会再多借用下李老师的图，hhh，但是仅限于整理，思路可有那么一点点不连贯，所以具体内容还是建议大家去看李老师的视频学习。

图4. Scaled Dot-Product Attention和Multi-Head Attention

1.3.2.1 self-attention：

图5. Self-attention

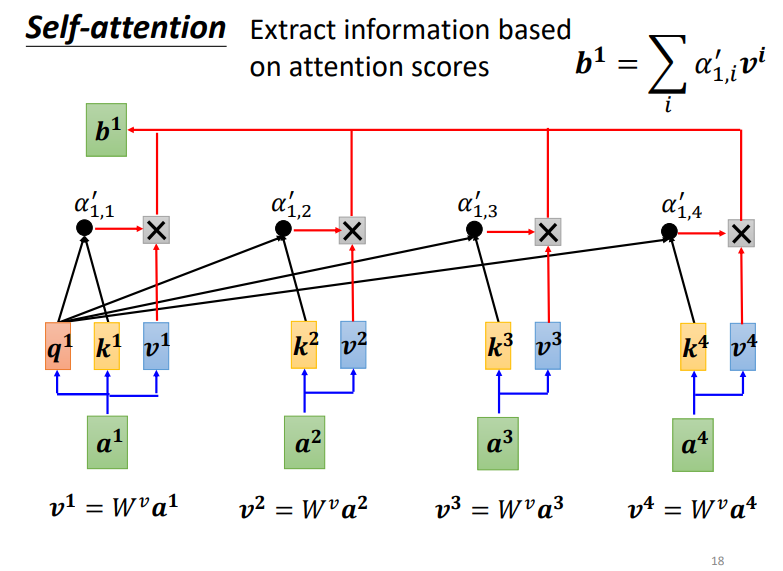
解释下图5.中的变量表示的意义，输入 $ A=[a_1, ….., a_n] $ ，每一个向量对应有一个$q^i, k^i, v^i $，其中q是query，k是key，v是value，是分别根据$ W^q\cdot{a^i}, W^k\cdot{a^i}, W^v\cdot{a^i} $得到的，而$ W^q, W^k, W^v$这三个就是模型要学习的参数，然后$ \alpha’_{i,j}=softmax(q^i\cdot{k^j})$ ，主要是用来表示两个向量的相关程度（内积值越大，余弦值越大，相似度越高）。

最终，$b^i=\sum_{i} \alpha’_{i,j} \cdot v^i$，这里说个我的小理解，i是作为q，而j是作为k。

最后的公式为：$Attention(Q,K,V)=QK^TV$

1.3.2.2 Scaled Dot-Product Attention：

图6. Scaled Dot-Product Attention

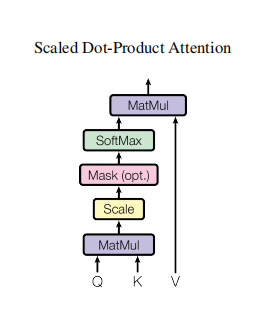
公式表示为：$ Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt{d_k}})V $

结合原论文中给出的结构和公式，来分析下这个attention，相比1.3.2.1中attention多除了一个$\sqrt{d_k}$，这个d就是dimension of k，而其实最后q、k、v最终的维度一般都是相同的，然后文章中提到了两种常用的注意力函数分别是additive attention和dot-product（这个就是1.3.2.1中的），当然了三者维度不同的话，也可以用additive attention，这里就不再详细展开了（留个坑）。

1.3.2.3 Multi-Head Attention：

图7. Multi-Head Attention

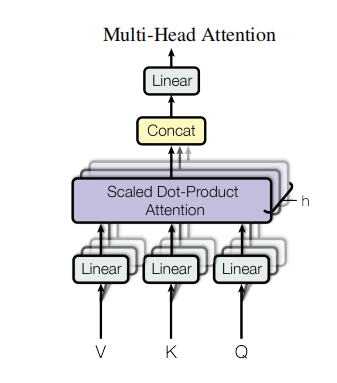
至于transformer中的Mutil-Head Aattention，也很简单，图7. 是原论文中的结构，这里说明下用它的一个原因，因为Scaled Dot-Product Attention没有可以学习的参数，只是通过点积来计算，因此为了提升模型对不同问题的特征进行分析的能力，就用了不同的线性映射，而最后所有线性映射再进行并行运算，原文中是用了8 heads。

图8. 2heads

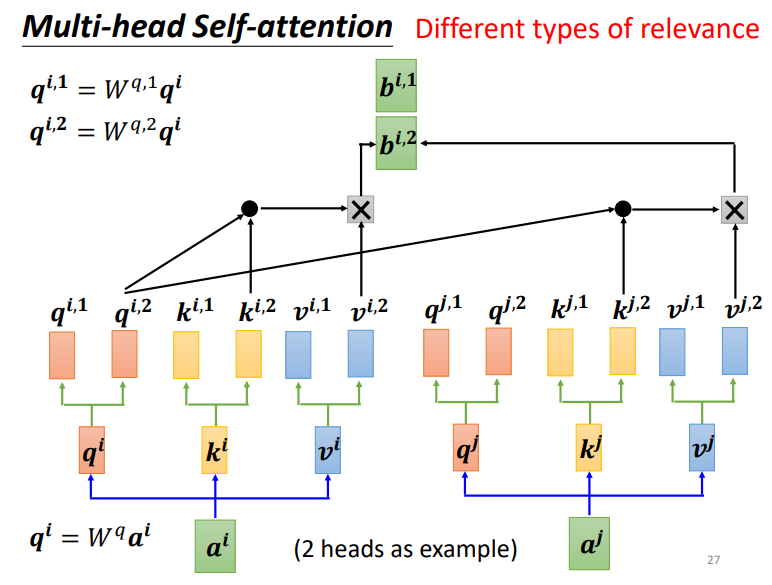
图8. 是2 heads的例子，其实就是将$q^i, k^i, v^i $以及 $b^i$ 变成了$q^{i,k}, k^{i,k}, v^{i,k}, b^{i,k}$，下面是具体实现的代码：

class MultiHeadAttention(nn.Module):
    """多头注意力"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 num_heads, dropout, bias=False, **kwargs):
        super(MultiHeadAttention, self).__init__(**kwargs)
        self.num_heads = num_heads
        self.attention = d2l.DotProductAttention(dropout)
        self.W_q = nn.Linear(query_size, num_hiddens, bias=bias)
        self.W_k = nn.Linear(key_size, num_hiddens, bias=bias)
        self.W_v = nn.Linear(value_size, num_hiddens, bias=bias)
        self.W_o = nn.Linear(num_hiddens, num_hiddens, bias=bias)
        
    def forward(self, queries, keys, values, valid_lens):
        # queries，keys，values:(batch_size, num_keys, num_hiddens)
    	# valid_lens:(batch_size, ) or (batch_size, num_keys)
    	# 输出的queries, keys, values:(batch_size*num_heads, num_keys, num_hiddens/num_heads)
        queries = transpose_qkv(self.W_q(queries), self.num_heads)
        keys = transpose_qkv(self.W_k(keys), self.num_heads)
        values = transpose_qkv(self.W_v(values), self.num_heads)
        
        if valid_lens is not None:
            # 在轴0，将第一项（标量或者矢量）复制num_heads次，
            # 然后如此复制第二项，然后诸如此类。
            valid_lens = torch.repeat_interleave(
                valid_lens, repeats=self.num_heads, dim=0)

        # output:(batch_size*num_heads, num_keys, num_hiddens/num_heads)
        output = self.attention(queries, keys, values, valid_lens)

        # output_concat:(batch_size, num_keys, num_hiddens)
        output_concat = transpose_output(output, self.num_heads)
        return self.W_o(output_concat)
    
def transpose_qkv(X, num_heads):
	"""为了多注意力头的并行计算而变换形状"""
    # X_in:(batch_size, num_keys, num_hiddens)
    # X_out:(batch_size, num_keys, num_heads, num_hiddens/num_heads)
    X = X.reshape(X.shape[0], X.shape[1], num_heads, -1)

    # X_out':(batch_size, num_heads, num_keys, num_hiddens/num_heads)
    X = X.permute(0, 2, 1, 3)

    # final_out:(batch_size*num_heads, num_keys, num_hiddens/num_heads)
    return X.reshape(-1, X.shape[2], X.shape[3])

def transpose_output(X, num_heads):
    """逆转transpose_qkv函数的操作"""
    # X_in:(batch_size*num_heads, num_keys, num_hiddens/num_heads)
    # X_out:(batch_size, num_heads, num_keys, num_hiddens/num_heads)
    X = X.reshape(-1, num_heads, X.shape[1], X.shape[2])
    
    # X_out':(batch_size, num_keys, num_heads, num_hiddens/num_heads)
    X = X.permute(0, 2, 1, 3)
    # output:(batch_size, num_keys, num_hiddens)
    return X.reshape(X.shape[0], X.shape[1], -1)

1.3.4 Position-Wise Feed-Forward Networks：

这个其实就是通过一个1×1的卷积核来升维，再一个1×1的卷积核来降维，中间再加一个ReLU，公式为：$FFN(x)=max(0,xW_1+b_1)W_2+b_2$，下面来看一下这部分的代码：

class PositionWiseFFN(nn.Module):
    """基于位置的前馈网络"""
    def __init__(self, ffn_num_input, ffn_num_hiddens, ffn_num_outputs,
                 **kwargs):
        super(PositionWiseFFN, self).__init__(**kwargs)
        self.dense1 = nn.Linear(ffn_num_input, ffn_num_hiddens)
        self.relu = nn.ReLU()
        self.dense2 = nn.Linear(ffn_num_hiddens, ffn_num_outputs)

    def forward(self, X):
        return self.dense2(self.relu(self.dense1(X)))

其实就是输入张量X（批量大小，时间序列长度，隐藏特征维度）被一个两层的MLP转换成输出张量Y（批量大小，时间序列长度，ffn_num_outputs)，其实可以直接把这个操作理解成将输出张量的最后一个维度给变了下。

1.3.5 Encoder Block：

图1.Encoder Block

对比上面的图1. 来理解下面的代码吧

class EncoderBlock(nn.Module):
    """transformer编码器块"""
    def __init__(self, key_size, query_size, value_size, num_hiddens,
                 norm_shape, ffn_num_input, ffn_num_hiddens, num_heads,
                 dropout, use_bias=False, **kwargs):
        super(EncoderBlock, self).__init__(**kwargs)
        # MHA
        self.attention = d2l.MultiHeadAttention(
            key_size, query_size, value_size, num_hiddens, num_heads, dropout,
            use_bias)
        # AN1
        self.addnorm1 = AddNorm(norm_shape, dropout)
        # FFN
        self.ffn = PositionWiseFFN(
            ffn_num_input, ffn_num_hiddens, num_hiddens)
        # AN2
        self.addnorm2 = AddNorm(norm_shape, dropout)
	
    def forward(self, X, valid_lens):
        # MHA+AN1
        Y = self.addnorm1(X, self.attention(X, X, X, valid_lens))
        # FFN+AN2
        return self.addnorm2(Y, self.ffn(Y))


class TransformerEncoder(d2l.Encoder):
    """transformer编码器"""
    def __init__(self, vocab_size, key_size, query_size, value_size,
                 num_hiddens, norm_shape, ffn_num_input, ffn_num_hiddens,
        num_heads, num_layers, dropout, use_bias=False, **kwargs):
        super(TransformerEncoder, self).__init__(**kwargs)
        # num_hiddens
        self.num_hiddens = num_hiddens
        self.embedding = nn.Embedding(vocab_size, num_hiddens)
        self.pos_encoding = d2l.PositionalEncoding(num_hiddens, dropout)
        self.blks = nn.Sequential()
        for i in range(num_layers):
            self.blks.add_module("block"+str(i),
                EncoderBlock(key_size, query_size, value_size, num_hiddens,
                             norm_shape, ffn_num_input, ffn_num_hiddens,
                             num_heads, dropout, use_bias))

    def forward(self, X, valid_lens, *args):
        # 因为位置编码值在-1和1之间，因此嵌入值乘以嵌入维度的平方根进行缩放，然后再与位置编码相加。
        # embedding, Pos_encoding
        X = self.pos_encoding(self.embedding(X) * math.sqrt(self.num_hiddens))
        self.attention_weights = [None] * len(self.blks)
        # N个Block
        for i, blk in enumerate(self.blks):
            X = blk(X, valid_lens)
            self.attention_weights[
                i] = blk.attention.attention.attention_weights
        #最终输出:(Batch_size, length, num_hiddens）
        return X

1.4 Decoder：

自回归，输入是上一层的输出

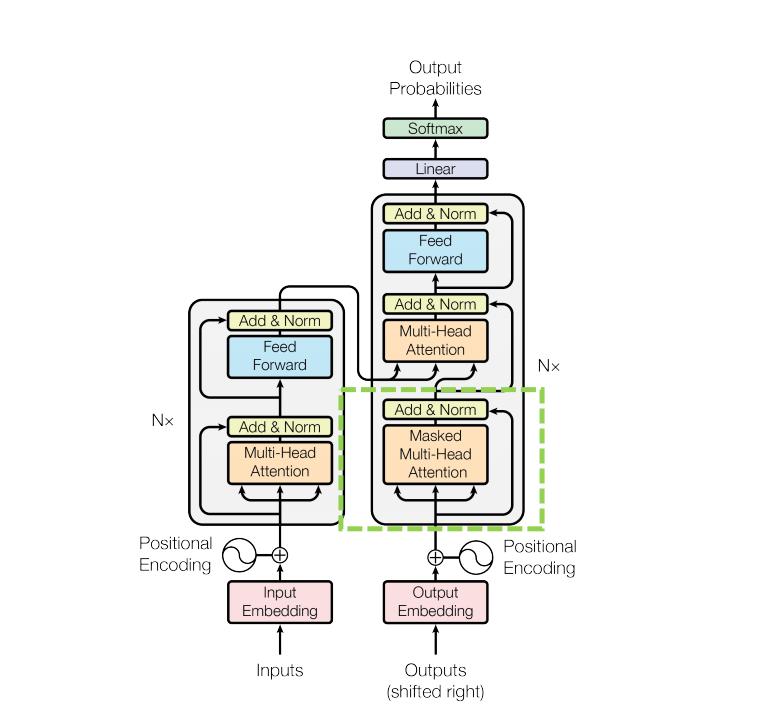
Transformer_1

图0. Transformer

其实从图0. 中，可以看出decoder的结构貌似和encoder有一部分很像，只是下面多了框框中的部分，Masked Multi-Head Attention + Add&Norm，下面来讲下这部分。

1.4.1 Masked Multi-Head Attention：

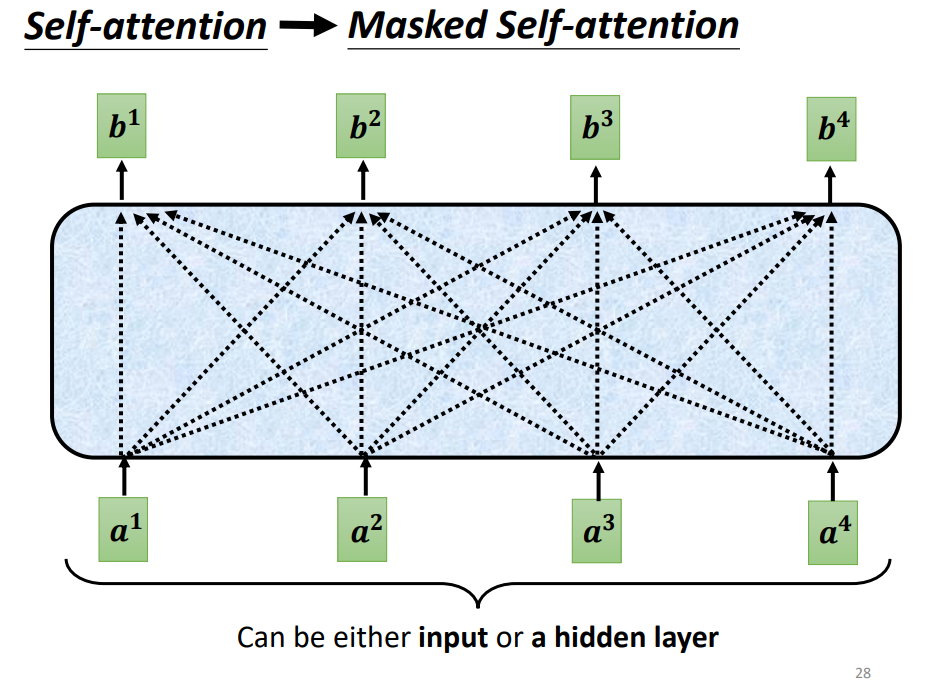
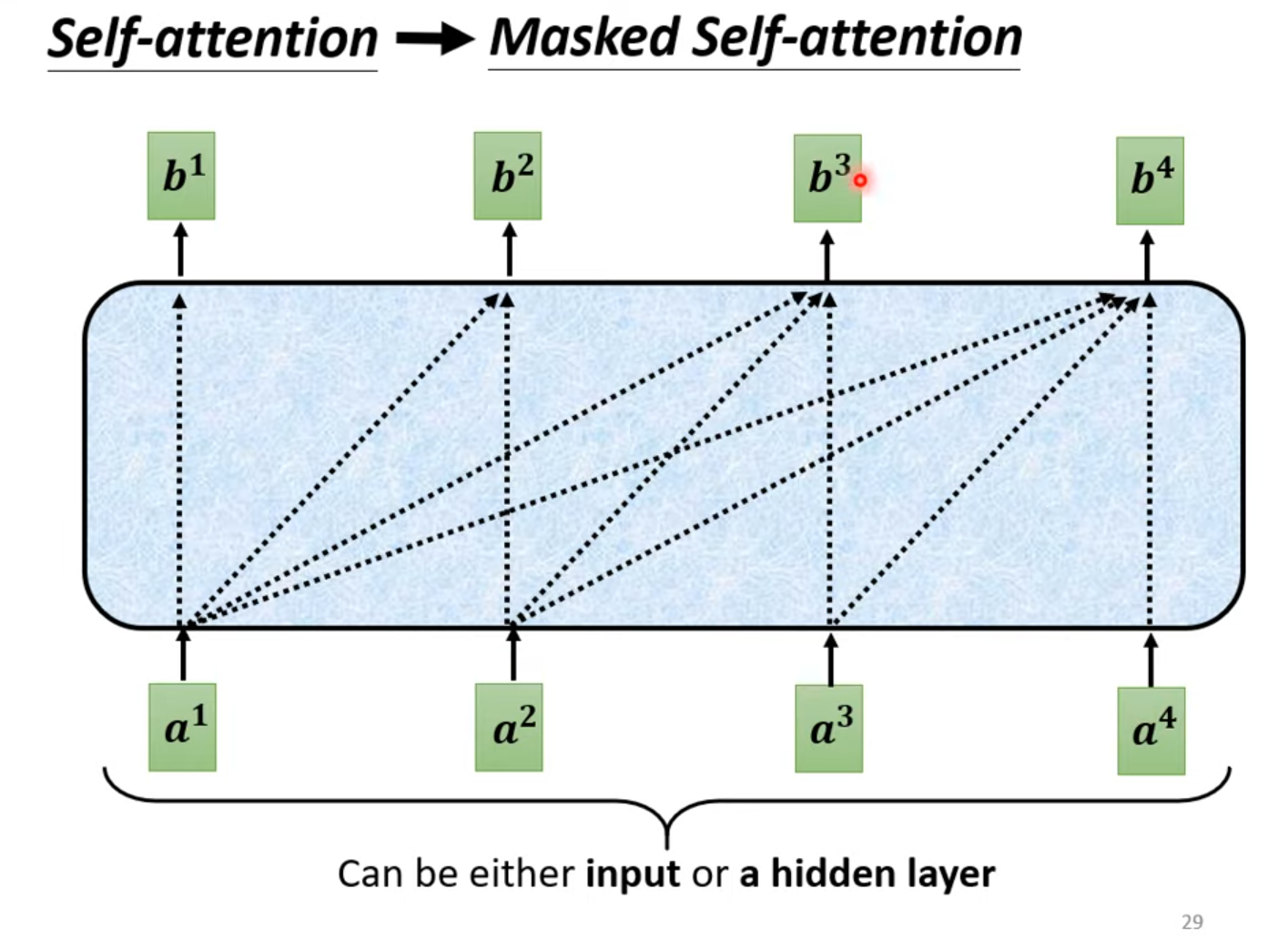
首先来看，其中的Masked Multi-Head Attention，对比9. attention和图10. 所示的Masked attention就比较容易理解了，因为当前的输入是有序列的$a^i$，而原始self-attention的操作产生$b^i$时，会考虑所有的$a^i$，Masked attention是不再考虑包括$a^{i+1}$在内的右边的输入。

图9. Self Attention

图10. Masked Self Attention

1.4.2 ：

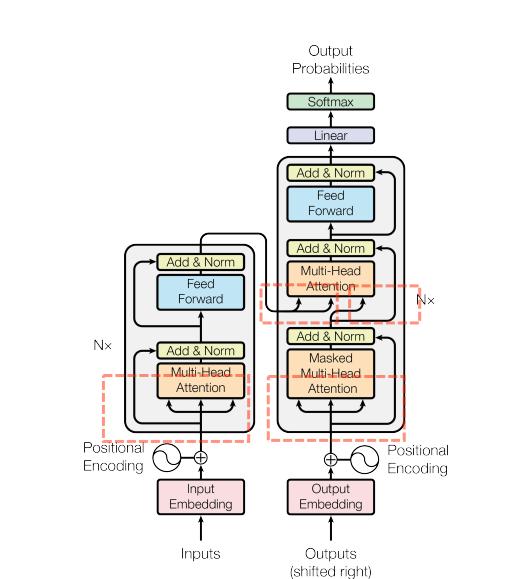
Transformer_2