Vision Transformer:
接着来开个ViT的新坑,论文链接: An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale。
因为Transformer的计算效率和可扩展性,该文采用了此结构(可参考之前的博文:Transformer),主要分为Embedding、Transformer Encoder、MLP Head三部分,下面就按这个顺序进行整理。
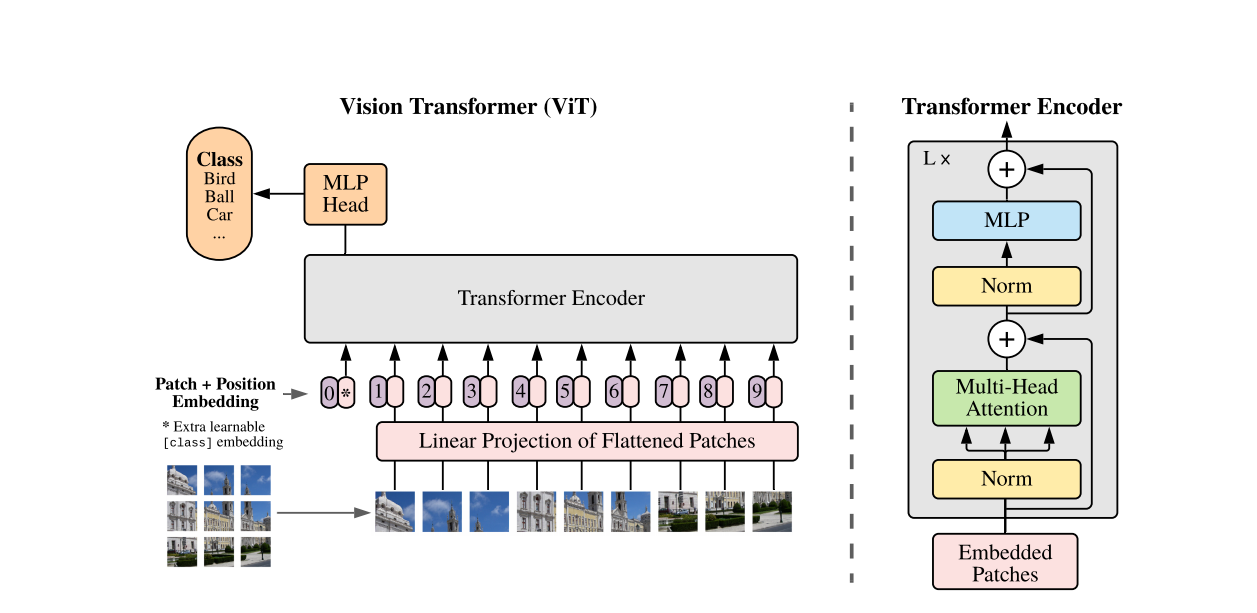
1. Embedding:
Transformer Encoder 的输入要求为token,也就是一个形状为$[num_token, token_dim]$的矩阵。
编码的具体流程参考下图中,对于形状为$[H, W, C]$的输入图像而言,被分成了很多的形状为$[P,P,C]$的块,可以算的最终块的数目为:$\frac{H\times W}{P\times P}$,所以总体形状变为$[\frac{H\times W}{P\times P},P\times P\times C]$,然后再经过一个线性映射总体形状变为$[\frac{H\times W}{P\times P}, D]$,此处的D是自定义的。
接下来,还需加入一个用于分类的cls,因此token形状变为$[\frac{H\times W}{P\times P}+1,P\times P\times C]$。
此外,为了保证块的位置信息,再在token中加上可以学习的位置编码参数,最终得到的token大小仍然是$[\frac{H\times W}{P\times P}+1,P\times P\times C]$。
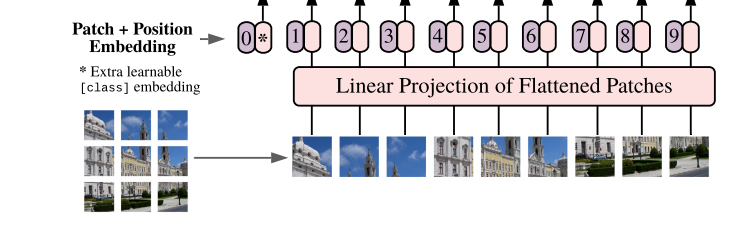
这里提一下,代码中切割patch可以用conv16×16 Stride=16的卷积操作来实现,而在position embedding后还需要经过一步dropout(emd_dropout)才进入了encoder block里面。
2. Transformer Encoder:
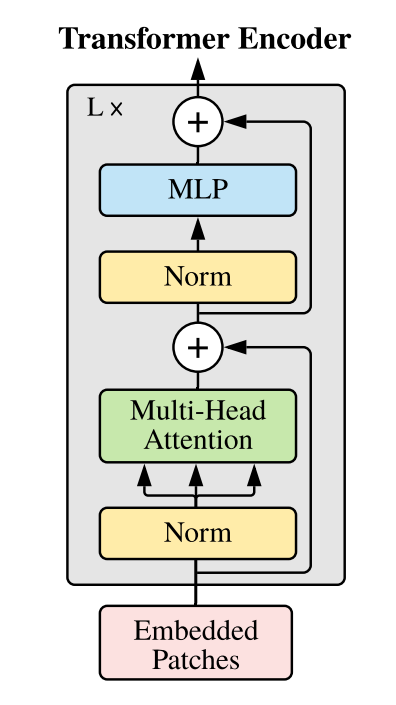
Encoder这里就和Transformer的Encoder差不多。值得注意的是这里每一层前,都要进行层归一化(Layer Norm,可以参考之前的博文:Batch Normalization)。此外,每层之后包含一个残差链接。而MLP那里也很简单,就是Linear->GELU->Linear->Dropout,其中第一个Linear会把输入节点翻成4倍,形状变为$[\frac{H\times W}{P\times P},P\times P\times C \times4]$,第二个Linear再把它缩小4倍。
从Transformer Encoder出来之后,在进入MLP head之前,还需要进入一个Layer Norm。
因此原文中将上述过程简单的用公式描述为:
\[\begin{align} &z_0 = [x_{class};x^1_pE;x^2_pE;\cdot\cdot\cdot;x^N_pE;]+E_{pos}, \qquad\qquad E\in R^{(P^2\cdot C)}, \quad E_{pos}\in R^{(N+1)\times D} \qquad\qquad \\ &z'_l=MSA(LN(z_{l-1}))+z_{l-1} \qquad\qquad l=1…L\qquad\qquad \\ &z_l=MLP(LN(z'_{l}))+z'_{l} \qquad\qquad l=1…L\qquad\qquad \\ &y = LN(z^0_L) \end{align}\]2.1 归纳偏置:
相比于CNN,ViT含有更少的图像归纳偏置,这种偏置被称为偏好更恰当,是因为学习算法必须有某种偏好,才能产生它认为正确的模型,换而言之就是算法在其假设空间内,进行选择的启示录或价值观。
CNN中,局部性、二维相邻结构以及平移同变性这些归纳偏置,是嵌入到每一层贯穿整个模型的。而ViT中只有MLP部分有局部性和平移同变性,且自注意力层是全局性的,此外二维相邻结构仅在切割图像为块和在微调时为不同分辨率图像调整位置编码时会使用到。
2.1.1 平移不变性/同变性:
这里简单整理下,平移不变性(Translation Invariance)和平移同变性(Translation Equivariance),就是一张图片中的主要内容发生了平移后,分别在图像分类和目标检测两种任务中体现的不同结果的原因。
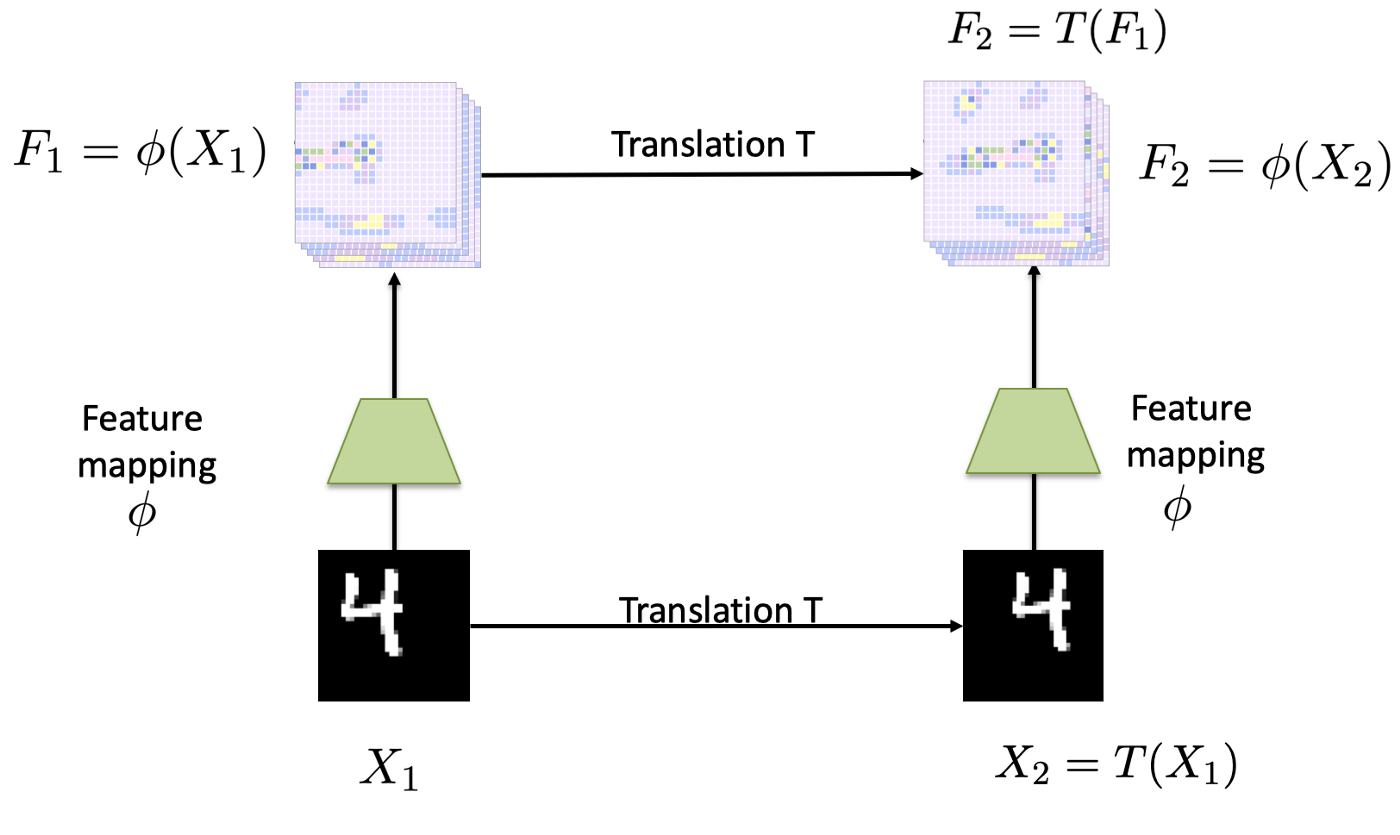
来看上面这张图,其中的$X_1$经过平移后得到$X_2$中,二者中的数字4的含义其实是一样的,而再经过相同的映射方法之后,得到的特征图$F_1$和$F_2$,仍然可以通过之前的平移操作实现转换。针对于分类任务,得到的分类结果是相同的,而检测任务中,二者的候选框却是不同的。
更具体的讲解可以参考这两篇文章关于平移不变性与平移相等性的理解与讨论、What is translation equivariance, and why do we use convolutions to get it?。
2.2 GELU:
高斯误差线性单元(Gaussian Error Linerar Units),(这一段是看网上博客整理的材料,没有去翻原论文,不保证准确性)就是在ReLU中引入了随机正则(Dropout)的思想,根据自身输入的情况来,来决定抛弃还是保留当前神经元。
函数形式:$GELU(x)=0.5x(1+tanh(\sqrt{2/\pi(x+0.044715x^3)}))$
3. MLP Head:
然后这个MLP Head感觉没啥可以讲的,就是一个线性层。
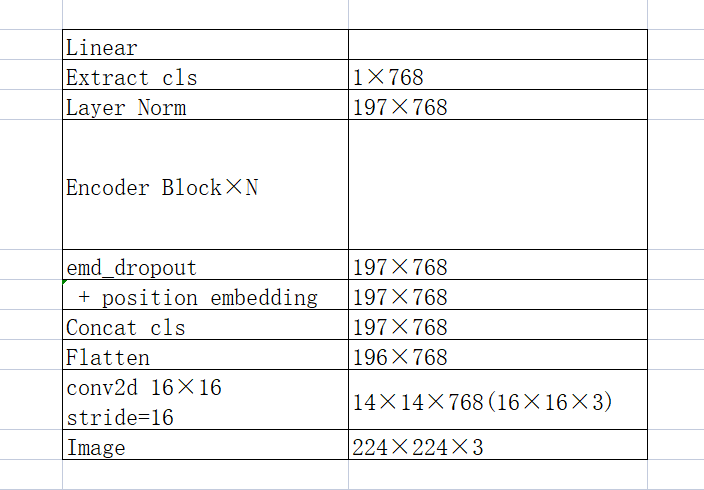
最后来一个表简单的理解一下整个网络结构。之后再详细补上代码等内容
文档信息
- 本文作者:Guoziyu
- 本文链接:https://mateguo1.github.io/2021/11/18/ViT/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)